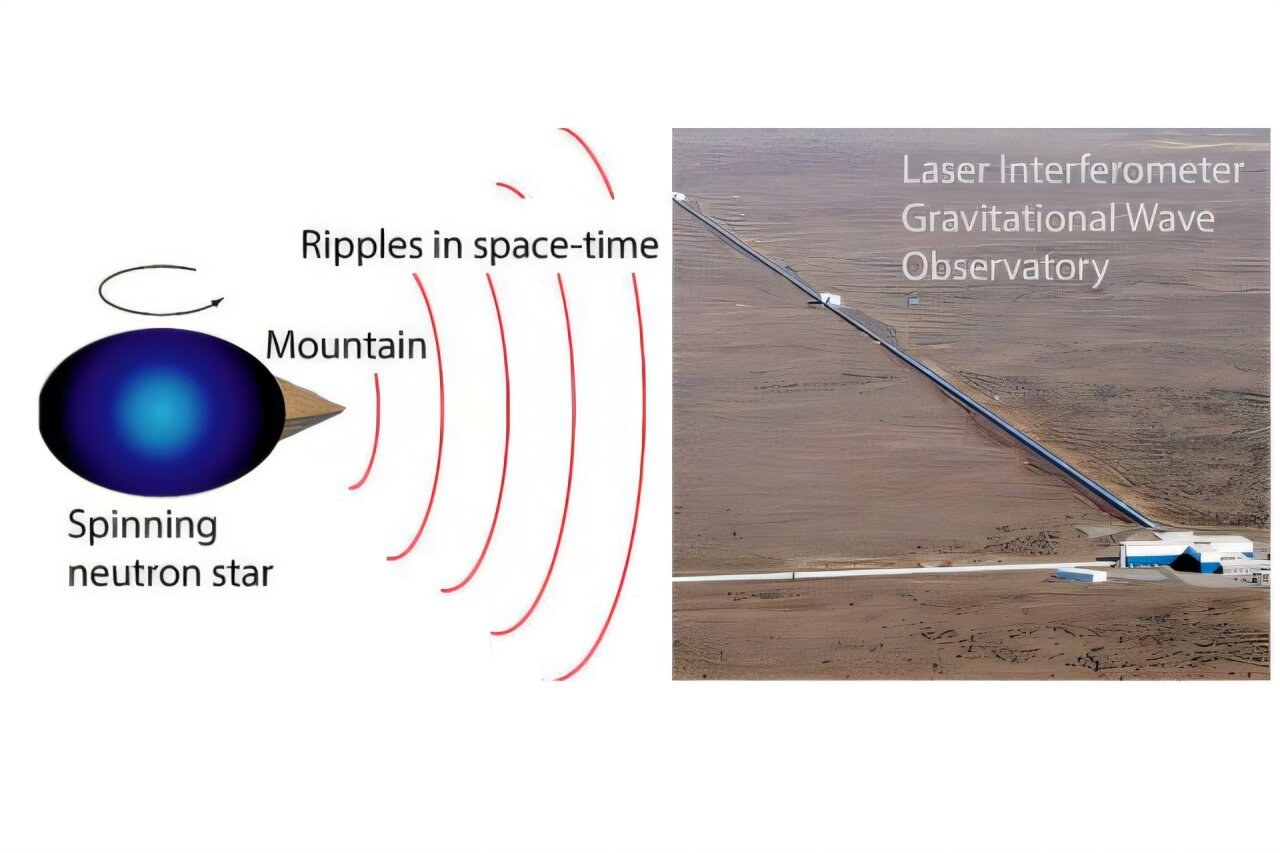
Neutron stars are among the most fascinating and enigmatic objects in the universe. These collapsed remnants of massive stars are incredibly dense, with a mass greater than the Sun compressed into a sphere just 10 to 20 kilometers across. A neutron star’s core is so dense that its material is far more compact than even the densest element on Earth, lead. In fact, a neutron star is a trillion times denser than lead. Despite their remarkable density and extreme gravity, many of the surface features of neutron stars remain poorly understood.
Nuclear theorists, however, have recently explored the possibility of mountains forming on neutron stars, inspired by the geological features of moons and planets within our own solar system. This idea suggests that, just as planetary bodies like Europa or Enceladus display surface features such as cracks and stripes due to internal dynamics, neutron stars may also experience similar deformations. These so-called “mountains” on neutron stars could be vastly different in size and impact than anything we observe on Earth.
The fundamental concept behind these potential neutron star mountains lies in their incredibly high density. Neutron stars are incredibly compact, and their surface features, if they exist, would be massive enough that their gravity would cause tiny oscillations in the fabric of space-time itself. The deformation of the star’s surface would, in turn, create ripples or oscillations in the fabric of space-time, known as gravitational waves. The study of these gravitational waves has become one of the leading ways to probe the properties of neutron stars and their extreme environments.
These gravitational waves, emitted by non-axisymmetric deformations—meaning uneven or lopsided features—of rotating neutron stars, could provide valuable insights into their structure. Just like the ridges, valleys, and cracks on planets and moons in our solar system are the result of their unique geological histories, it is hypothesized that neutron stars, too, might exhibit similar features.
In particular, there are interesting analogies between the surface features of certain moons in our solar system and the potential mountains on neutron stars. Moons such as Europa (one of Jupiter’s largest moons) and Enceladus (one of Saturn’s moons) possess thin crusts that sit atop deep oceans. Similarly, the planet Mercury has a thin crust over a large metallic core. These moons, as well as Mercury, show various surface features resulting from the internal dynamics of these bodies, such as linear features, tiger-like stripes, and curved, step-like structures. It’s not too far of a leap to suggest that neutron stars, with their similarly dense and active interiors, might produce analogous mountain-like features, albeit much more extreme.
The notion of “mountains” on neutron stars arises from theoretical models that suggest that the star’s crust material might exhibit anisotropic properties. Anisotropy refers to the directional dependence of a material’s properties, meaning that the material behaves differently depending on the direction in which it is stressed. If the crust of a neutron star is anisotropic, it could undergo a mountain-like deformation as the star spins. The faster the neutron star rotates, the more pronounced the deformation may become. This provides an intriguing explanation for the maximum spin observed in certain neutron stars, and it could also help explain why some types of neutron stars, specifically millisecond pulsars, exhibit minimal deformation despite emitting radio waves.
These mountains could hold the key to understanding the extreme physics of neutron stars, which are some of the densest objects in the universe, second only to black holes. The possibility of observing the gravitational waves from these mountains opens up a new window into the inner workings of neutron stars. Gravitational waves are ripples in space-time caused by massive objects accelerating, and neutron stars with significant surface deformations would generate continuous gravitational waves as they spin.
The Laser Interferometer Gravitational-Wave Observatory (LIGO), which has already detected gravitational waves from events like black hole mergers, is now focused on searching for these continuous gravitational waves generated by neutron stars. However, detecting these ripples is no easy feat. Gravitational waves are incredibly weak and require highly sensitive equipment to detect. LIGO’s detectors are carefully tuned to specific frequencies that match the predicted characteristics of the waves coming from neutron stars, making the search challenging but potentially groundbreaking.
The first detection of continuous gravitational waves from neutron stars would be a monumental achievement, providing unprecedented insight into their internal structure and offering new information about the densest objects in the universe. Beyond providing a deeper understanding of neutron stars, the detection of these waves could serve as a sensitive test of the fundamental laws of physics. For instance, it might allow scientists to test general relativity in ways never before possible, offering crucial data that could either reinforce or challenge our current understanding of space-time and gravity.
Moreover, these discoveries would open a completely new area of observational astronomy, one that is currently unexplored. The study of continuous gravitational waves could enable scientists to directly measure and analyze the internal dynamics of neutron stars, including how their material responds to the extreme conditions inside these celestial bodies. This could lead to breakthroughs in our understanding of neutron star matter, a substance that cannot be replicated on Earth due to the extreme conditions required to create it.
Reference: J. A. Morales et al, Anisotropic neutron star crust, solar system mountains, and gravitational waves, Physical Review D (2024). DOI: 10.1103/PhysRevD.110.044016. On arXiv: DOI: 10.48550/arxiv.2309.04855